We all have read the story of Sir Srinivasa Ramanujan in our school time.
This is refreshing revision to it :
This is what Ramanujan meant.
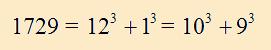
After Hardy related this incident to his colleagues, this number became well known and was called as Ramanujan Number.
Later on, numbers having similar property were all called as Ramanujan Numbers & the problem of finding such numbers came to be known as TaxiCab(2) problem. That is, solution to TaxiCab(2) yielded numbers of the kind
Here are a few numbers of this kind :
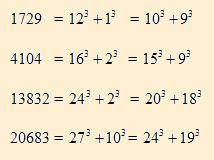
Numbers of the kind a^3 + b^3 = m^3 + n^3 = x^3 + y^3 are now known as Ramanujan Triples. The corresponding problem is known as TaxiCab(3).
Numbers of the kind a^3 + b^3 = c^3 + d^4 = w^3 + x^3 = y^3 + z^3 are known as Ramanujan Quadruples or corresponding problem is known as TaxiCab(4), and so on.
Moral of the story :
Infinite RESPECT is actually defined in the world !
This is refreshing revision to it :
Srinivasa Ramanujan (22 December 1887 – 26 April 1920) was
a renowned Indian Mathematician. Inspite of having no formal training
in pure mathematics, Ramanujan made substantial contributions in the
areas of mathematical analysis, number theory, infinite series and
continued fractions. He independently compiled nearly 3500 results
during his short life time.
1729 came to be known as Ramanujan number, after an interesting incident that took place between Ramanujan & his mentor, G. H. Hardy.
Hardy was paying a visit to Ramanujan, who was ill and undergoing treatment at Putney (London). Hardy mentioned to him that he rode a taxi cab, whose number was 1729. "...the number seemed to me rather a dull one", he added.
It is said about Ramanujan that the numbers 1 - 10000 were his "personal friends". He could effortlessly tell you their factors, divisors, how the number can be split & the each part of the number can be squared/cubed, etc. to produce interesting numbers, and much more.
Interestingly enough, Ramanujan replied to Hardy's comment, saying that 1729 is not a dull number at all. It is the smallest number that can be written as sum of 2 cubes, in 2 different ways.
1729 came to be known as Ramanujan number, after an interesting incident that took place between Ramanujan & his mentor, G. H. Hardy.
Hardy was paying a visit to Ramanujan, who was ill and undergoing treatment at Putney (London). Hardy mentioned to him that he rode a taxi cab, whose number was 1729. "...the number seemed to me rather a dull one", he added.
It is said about Ramanujan that the numbers 1 - 10000 were his "personal friends". He could effortlessly tell you their factors, divisors, how the number can be split & the each part of the number can be squared/cubed, etc. to produce interesting numbers, and much more.
Interestingly enough, Ramanujan replied to Hardy's comment, saying that 1729 is not a dull number at all. It is the smallest number that can be written as sum of 2 cubes, in 2 different ways.
This is what Ramanujan meant.
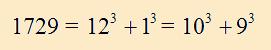
After Hardy related this incident to his colleagues, this number became well known and was called as Ramanujan Number.
Later on, numbers having similar property were all called as Ramanujan Numbers & the problem of finding such numbers came to be known as TaxiCab(2) problem. That is, solution to TaxiCab(2) yielded numbers of the kind
a^3 + b^3 = c^3 + d^3
Here are a few numbers of this kind :
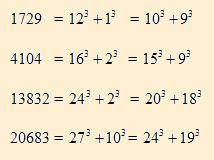
Numbers of the kind a^3 + b^3 = m^3 + n^3 = x^3 + y^3 are now known as Ramanujan Triples. The corresponding problem is known as TaxiCab(3).
Numbers of the kind a^3 + b^3 = c^3 + d^4 = w^3 + x^3 = y^3 + z^3 are known as Ramanujan Quadruples or corresponding problem is known as TaxiCab(4), and so on.
Moral of the story :
Infinite RESPECT is actually defined in the world !

No comments:
Post a Comment